Matematika himpunan elemen dan bilangan

Matematika (Himpunan, Elemen, dan Bilangan)

Himpunan dan Elemen 

1.) Pengertian Himpunan

 Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas. Benda atau objek dalam himpunan disebut elemen atau anggota himpunan. Dari definisi tersebut, dapat diketahui objek yang termasuk anggota himpunan atau bukan.

Contoh himpunan:
• Himpunan warna lampu lalu lintas, anggota himpunannya adalah merah, kuning, dan hijau.
• Himpunan bilangan prima kurang dari 10, anggota himpunannya adalah 2, 3, 5, dan 7.
Contoh bukan himpunan:
• Kumpulan baju-baju bagus.
• Kumpulan makanan enak.

2..)Jenis-Jenis Himpunan

1. Himpunan Bagian (Subset).

Himpunan A dikatakan  himpunan  bagian  (subset)  dari  himpunan B ditulis A ⊂ B ”, jika setiap anggota A merupakan anggota dari B.

Syarat :

A ⊂ B, dibaca : A himpunan bagian dari B

A ⊂ B, dibaca : A bukan himpunan bagian dari B

B  ⊂  A dibaca : B bukan himpunan bagian dari A

B  ⊂  A dibaca : B bukan himpunan bagian dari A

Contoh :

Misal   A = { 1,2,3,4,5 } dan B = { 2,4} maka  B ⊂ A.

2. Himpunan Kosong (Nullset)

Himpunan kosong adalah himpunan yang tidak mempunyai unsur anggota yang sama sama sekali.

Syarat :

Himpunan kosong = A atau { } Himpunan kosong adalah tunggal

Himpunan kosong merupakan himpunan bagian dari setiap himpunan

Perhatikan : himpunan kosong tidak boleh di nyatakan dengan { 0 }.

Sebab : { 0 } ≠ { }

3. Himpunan Semesta

Himpunan semesta biasanya dilambangkan dengan “U” atau “S” (Universum) yang berarti himpunan yang memuat semua anggota yang dibicarakan atau kata lainya himpunan dari objek yang sedang dibicarakan.

4. Himpunan Sama (Equal)

Bila setiap anggota himpunan A juga merupakan anggota himpunan B, begitu pula sebaliknya.dinotasikan dengan A=B

Syarat : Dua buah himpunan anggotanya harus sama.

Contoh :

A ={ c,d,e}    B={ c,d,e }   Maka A = B

5. Himpunan Lepas

Himpunan lepas adalah suatu himpunan yang anggota-anggotanya tidak ada yang sama.

Contoh  C = {1, 3, 5, 7}   dan  D = {2, 4, 6}  Maka himpunan C dan himpunan D saling lepas.

Catatan : Dua himpunan yang tidak kosong dikatakan saling lepas jika kedua himpunan itu tidak mempunyai satu pun anggota yang sama

6. Himpunan Komplemen (Complement set)

Himpunan komplemen dapat di nyatakan dengan notasi A^C . Himpunan komplemen jika di misalkan S = {1,2,3,4,5,6,7} dan A = {3,4,5} maka A ⊂ U. Himpunan {1,2,6,7} juga merupakan komplemen, jadi A^C = {1,2,6,7}. Dengan notasi pembentuk himpunan ditulis :

A^C = {x│x Є U, x Є A}

7. Himpunan Ekuivalen (Equal Set)

Himpunan ekuivalen adalah himpunan yang anggotanya sama banyak dengan himpunan lain.

Syarat : Bilangan cardinal dinyatakan dengan notasi n (A) A≈B, dikatakan sederajat atau ekivalen, jika himpunan A ekivalen dengan himpunan B,

Contoh :

A = { w,x,y,z }→n (A) = 4

B = {  r,s,t,u   } →n  (B) = 4

Maka n (A) =n (B) →A≈B

Bilangan

Bilangan adalah kumpulan angka yang menempati urutan dari sebelah kanan sebagai nilai satuan, puluhan, ratusan, ribuan dan seterusnya. Sedangkan pengertian bilangan menurut wikipedia yaitu suatu konsep matematika yang dipergunakan untuk pencacahan serta pengukuran.

Simbol dan lambang yang dipakai untuk mewakili suatu bilangan disebut dengan angka atau lambang bilangan. Didalam matematika, konsep bilangan selama bertahun-tahun lamanya telah diperluas meliputi bilangan nol, bilangan negatif, bilangan rasional, bilangan irasional, serta bilangan kompleks.

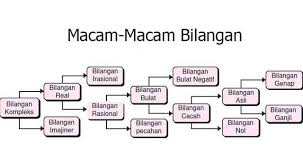
Macam-macam Bilangan

1. Bilangan Cacah
Bilangan cacah adalah bilangan yang dimulai dari angka 0 dan selalu bertambah 1 dengan bilangan setelahnya.
contoh : 0, 1, 2, 3, 4 dan seterusnya.

 2.Bilangan Asli
Bilangan asli adalah bilangan yang dimulai dari angka 1 dan bertambah 1.
contoh : 1, 2, 3, 4, 5 dan seterusnya.

3. Pecahan Biasa
Pecahan biasa adalah bilangan yang dapat dinyatakan dalam a/b, dengan a dan b merupakan bilangan bulat dan b ≠ 0. Bilangan a disebut dengan pembilang sedangkan bilangan b disebut dengan penyebut.
contoh : 7/3, 1/3, 5/66

4. Bilangan Bulat
Bilangan bulat adalah himpunan bilangan bulat negatif, bilangan nol dan bilangan bulat positif.
contoh : ...., -3, -2, -1, 0, 1, 2, 3, .....

5. Bilangan Prima
Bilangan prima adalah seluruh bilangan asli yang hanya mempunyai faktor pembagi satu dan bilangan itu sendiri atau bilangan yang hanya dapat dibagi oleh 1 dan bilangan itu sendiri.
contoh : 2, 3, 5, 7, 11,....

6. Bilangan Komposit
Bilangan komposit adalah seluruh bilangan asli kecuali 1 dan tidak termasuk dalam bilangan prima.
contoh : 4, 6, 8, 9, 10,.....

7. Bilangan Rasional.
Bilangan rasional adalah semua bilangan yang dinyatakan dalam bentuk a/b, dengan a dan b merupakan anggota bilangan bulat serta b ≠ 0.

8. Bilangan Irasional
Bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk a/b, dengan a dan b merupakan anggota bilangan bulat serta b ≠ 0. merupakan kebalikan bilangan rasional.

9. Bilangan Riil
Bilangan riil adalah merupakan gabungan dari bilangan rasional dengan bilangan irasional.

10. Bilangan Desimal
Bilangan desimal adalah bilangan yang mempunyai bentuk ciri ciri antar bilangan dipisahkan dengan tanda koma sebanyak satu.

11. Bilangan Pangkat
Bilangan pangkat adalah bilangan yang dihasilkan dari mengalikan sebuah bilangan beberapa kali.

12. Bilangan Imajiner
Bilangan Imajiner atau yang dikenal dengan bilangan khayal adalah bilangan yang memiliki sifat  i2 = −1 . Dengan kata lain, bilangan tersebut memiliki akar negatif.
Contoh : I = { i, 4i, 5i, ….. }

13 . Bilangan Kompleks
Bilangan kompleks ialah bilangan yang dinotasikan oleh a+bi , dimana a dan b ialah bilangan riil, dan i ialah suatu bilangan imajiner dimana i 2 = −1. Bilangan riil a disebut juga bagian riil dari bilangan kompleks, dan bilangan real b disebut bagian imajiner. Bila dalam satu bilangan kompleks, nilai b ialah 0, jadi bilangan kompleks itu menjadi sama juga dengan bilangan real a.

Untuk contoh, 3 + 2i merupakan bilangan kompleks dengan bagian riil 3 dan bagian imajiner 2i.

14. Bilangan Genap
Bilangan Genap adalah bilangan yang dapat dinyatakan dalam bentuk 2n dan bilangan itu habis dibagi dengan bilangan 2.
Contoh: {2, 4, 6, 8, 10, 12, ….}

15. Bilangan Ganjil
Bilangan Ganjil adalah bilangan yang dapat dinyatakan dalam bentuk 2n – 1 dan tidak habis dibagi dengan bilangan 2.
Contoh: {-3, -1, 1, 3, 5, 7, 9, 11, 13, 15, … }

16. Bilangan Nol
Bilangan 0 adalah satu angka kosong (0) untuk mewakili angka di angka. Peranan terpenting angka 0 ialah menjadi identitas untuk bilangan real, bulat, dan aljabar yang lain.

17. Bilangan Negatif
Bilangan negatif ialah suatu bilangan yang mempunyai nilai minus (-) atau negatif.
Contoh: { dan seterusnya -5, -4, -3, -2, -1 }